U1Ch1L3: Finding Patterns and Writing Protocols

Purpose: Students will begin to focus on representing numeric values using an infinite Binary Number System.

Challenge #1: How many Combinations Can Be Made From Just 2 Shapes? (Handout)
Using the 2 shapes shown here, how many combinations can be assembles without repeating? In your Journals, begin assembling the combinations.

As an example, below is the first two combinations I came up with. Now it is up to you to discover the total number of combinations that can be assembled.

Total Number:                              

Challenge #2: How many Combinations Can be Made From These 3 Shapes? (Handout)

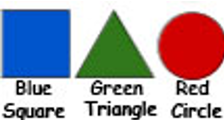
Using the 3 shapes shown hear, how many combinations can be assembled without repeating? Go to the Dry Erase Board and begin assembling combinations.

As an example, below is the first six combinations I came up with. Now it is up to you to discover the total number of combinations that can be assembled.

Total Number:                              

Challenge #3: Finding Patterns & Writing Protocols? (Handout)
Step back and view the geometric shape combinations that you assembled. Was there a particular way that you organized it so that you could come to a final answer? Do you see any patterns? If not, then rearrange the shapes to create a pattern.
Draw your pattern below left (Ask Instructor for colored pencils). Then write a protocol or guideline that will allow anyone to easily recreate your pattern – below right. When complete, hand this page to the instructor. The instructor will fold the page so that the image of the pattern will be hidden behind the protocol. The instructor will hand your protocol to one of your classmates so that when they follow your basic instructions, they should be able to easily recreate the pattern that you discovered. Finally, your classmate will unfold the page to see your pattern and can then compare it to the one they drew.